Wieferich prime
| Named after | Arthur Wieferich |
|---|---|
| Publication year | 1909 |
| Author of publication | Wieferich, A. |
| Number of known terms | 2 |
| Subsequence of | Crandall numbers[1] Wieferich numbers[2] near-Wieferich primes |
| First terms | 1093, 3511 |
| Largest known term | 3511 |
| OEIS index | A001220 |
In number theory, a Wieferich prime is a prime number p such that p2 divides 2p − 1 − 1,[3] therefore connecting these primes with Fermat's little theorem, which states that every odd prime p divides 2p − 1 − 1. Wieferich primes were first described by Arthur Wieferich in 1909 in works pertaining to Fermat's last theorem, at which time both of Fermat's theorems were already well known to mathematicians.[4][5]
Despite a number of extensive searches, the only known Wieferich primes to date are 1093 and 3511 (sequence A001220 in OEIS).
Contents |
Properties
Connection with Fermat's last theorem
The following theorem connecting Wieferich primes and Fermat's last theorem was proven by Wieferich in 1909:[6]
- Let p be prime, and let x, y, z be integers such that xp + yp + zp = 0. Furthermore, assume that p does not divide the product xyz. Then p is a Wieferich prime.
The above case (where p does not divide any of x, y or z) is commonly known as the first case of Fermat's Last Theorem (FLTI).[7][8] In 1910, Mirimanoff expanded[9] the theorem by showing that, if the preconditions of the theorem hold true for some prime p, then p2 must also divide 3p − 1 − 1. Morishima further proved that p2 must actually divide mp − 1 − 1 for every prime m ≤ 31.[10] Granville and Monagan extended the proof to all m ≤ 89.[11]
Connection with the abc conjecture
A non-Wieferich prime is a prime p satisfying 2p − 1 ≢ 1 (mod p2). Silverman showed in 1988 that if the abc conjecture holds, then there exist infinitely many non-Wieferich primes.[12] Numerical evidence suggests that very few of the prime numbers in a given interval are Wieferich primes. A proof of the abc conjecture would not automatically prove that there are only finitely many Wieferich primes, since the set of Wieferich primes and the set of non-Wieferich primes could possibly both be infinite and the finiteness or infiniteness of the set of Wieferich primes would have to be proven separately.
Connection with Mersenne and Fermat primes
It is known that the nth Mersenne number Mn = 2n − 1 is prime only if n is prime. Fermat's little theorem implies that if p > 2 is prime, then Mp−1 (= 2p − 1 − 1) is always divisible by p. Since Mersenne numbers of prime indices Mp and Mq are co-prime,
-
- A prime divisor p of Mq, where q is prime, is a Wieferich prime if and only if p2 divides Mq.[13]
Thus, a Mersenne prime cannot also be a Wieferich prime. A notable open problem is to determine whether or not all Mersenne numbers of prime index are square-free. If a Mersenne number Mq is not square-free, i.e., there exists a prime p for which p2 divides Mq, then p is a Wieferich prime. Therefore, if there are only finitely many Wieferich primes, then there will be at most finitely many Mersenne numbers that are not square-free. It was observed that M1092 is divisible by 10932 and M3510 is divisible by 35112.[14]
Similarly, if p is prime and p2 divides some Fermat number Fn = 22n + 1, then p must be a Wieferich prime.[15]
Binary periodicity of p-1
Johnson observed[16] that the two known Wieferich primes are one greater than numbers with periodic binary expansions (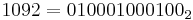 ;
; 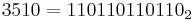 ). The Wieferich@Home project searches for Wieferich primes by testing numbers that are one greater than a number with a periodic binary expansion, but up to a "bit pseudo-length" of 3500 of the tested binary numbers generated by combination of bit strings with a bit length of up to 24 it has not found a new Wieferich prime.[17]
). The Wieferich@Home project searches for Wieferich primes by testing numbers that are one greater than a number with a periodic binary expansion, but up to a "bit pseudo-length" of 3500 of the tested binary numbers generated by combination of bit strings with a bit length of up to 24 it has not found a new Wieferich prime.[17]
Equivalent congruences
Wieferich primes can be defined by other congruences equivalent to the one usually used. If p is a Wieferich prime, we can multiply both sides of the congruence 2p-1 ≡ 1 (mod p2) with 2 to get 2p ≡ 2 (mod p2). Thus a Wieferich prime satisfies 2p2 ≡ 2 (mod p2), since it must satisfy 2kp ≡ 2 (mod p2) for all integers k ≥ 1.
History and search status
| Are there any Wieferich primes other than 1093 and 3511? |
In 1902 W. F. Meyer proved a theorem about solutions of the congruence ap − 1 ≡ 1 (mod pr). [18] Later in that decade Arthur Wieferich showed specifically that if the First Case of Fermat's Last Theorem has solutions for an odd prime exponent, then that prime must satisfy that congruence for a = 2 and r = 2. In other words, if there exist solutions to xp + yp + zp = 0 in integers x, y, z and p an odd prime with p ∤ xyz, then p satisfies 2p − 1 ≡ 1 (mod p2).
The only known Wieferich primes 1093 and 3511 were found by W. Meissner in 1913[19] and N. G. W. H. Beeger in 1922,[20] respectively. Around 1980, Lehmer was able to reach the search limit of 6×109.[21] This limit was extended to over 2.5×1015 in 2006[22], finally reaching 3×1015. It is now known, that if any other Wieferich primes exist, they must be greater than 6.7×1015.[23] The search for new Wieferich primes is currently performed by the distributed computing project Wieferich@Home. Another search is performed by the PrimeGrid project.[24]
It has been conjectured that only finitely many Wieferich primes exist.[3] It has also been conjectured (as for Wilson primes) that infinitely many Wieferich primes exist, and that the number of Wieferich primes below x is approximately log log x, which is a heuristic result that follows from the plausible assumption that for a prime p, the (p − 1)-th degree roots of unity modulo p2 are uniformly distributed in the multiplicative group of integers modulo p2.[25]
Generalizations
Near-Wieferich primes
A prime p satisfying the congruence 2(p−1)/2 ≡ ±1 + Ap (mod p2) with small |A| is commonly called a near-Wieferich prime (sequence A195988 in OEIS).[25][26] Near-Wieferich primes with A = 0 represent Wieferich primes. Recent searches, in addition to their primary search for Wieferich primes, also tried to find near-Wieferich primes.[23][27] The following table lists all near-Wieferich primes with |A| ≤ 10 in the interval [1×109, 3×1015]. This search bound was reached in 2006 in a search effort by P. Carlisle, R. Crandall and M. Rodenkirch.[22][28]
| p | 1 or −1 | A |
|---|---|---|
| 3520624567 | +1 | −6 |
| 46262476201 | +1 | +5 |
| 47004625957 | −1 | +1 |
| 58481216789 | −1 | +5 |
| 76843523891 | −1 | +1 |
| 1180032105761 | +1 | −6 |
| 12456646902457 | +1 | +2 |
| 134257821895921 | +1 | +10 |
| 339258218134349 | −1 | +2 |
| 2276306935816523 | −1 | −3 |
Dorais and Klyve[23] used a different definition of a near-Wieferich prime, defining it as a prime p with small value of 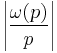 where
where 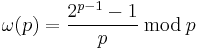 is the Fermat quotient of p modulo p (the modulo operation here gives the residue with the smallest absolute value). The following table lists all primes p ≤ 6.7 × 1015 with
is the Fermat quotient of p modulo p (the modulo operation here gives the residue with the smallest absolute value). The following table lists all primes p ≤ 6.7 × 1015 with 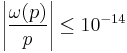 .
.
| p | 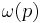 |
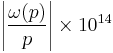 |
|---|---|---|
| 1093 | 0 | 0 |
| 3511 | 0 | 0 |
| 2276306935816523 | +6 | 0.264 |
| 3167939147662997 | −17 | 0.537 |
| 3723113065138349 | −36 | 0.967 |
| 5131427559624857 | −36 | 0.702 |
| 5294488110626977 | −31 | 0.586 |
| 6517506365514181 | +58 | 0.890 |
Base-a Wieferich primes
A Wieferich prime base a is a prime p that satisfies
- ap − 1 ≡ 1 (mod p2).[29]
Such a prime cannot divide a, since then it would also divide 1.
Wieferich pairs
A Wieferich pair is a pair of primes p and q that satisfy
- pq − 1 ≡ 1 (mod q2) and qp − 1 ≡ 1 (mod p2)
so that a Wieferich prime p ≡ 1 (mod 4) will form such a pair (p, 2): the only known instance in this case is p = 1093. There are 6 known Wieferich pairs.[30]
Wieferich numbers
A Wieferich number is an odd integer w ≥ 3 satisfying the congruence 2φ(w) ≡ 1 (mod w2). If Wieferich number w is prime, then it is a Wieferich prime. The first few Wieferich numbers are:
- 1093, 3279, 3511, 7651, 10533, 14209, 17555, 22953, 31599, 42627, 45643, … (sequence A077816 in OEIS)
It can be shown that if there are only finitely many Wieferich primes, then there are only finitely many Wieferich numbers. In particular, if the only Wieferich primes are 1093 and 3511, then there exist exactly 104 Wieferich numbers, which matches the number of Wieferich numbers currently known.[2]
See also
- Wall–Sun–Sun prime - a hypothetical type of prime number defined in the study of Fermat's last theorem (FLT)
- Wolstenholme prime - another type of prime number which in the broadest sense also resulted from the study of FLT
- List of near Wieferich primes - lists all near Wieferich primes up to 3×1015
- PrimeGrid
References
- ^ Franco, Z.; Pomerance, C. (1995), "On a conjecture of Crandall concerning the qx+1 problem", Math. Of Comput. (American Mathematical Society) 64 (211): 1333–1336, doi:10.2307/2153499, http://www.math.dartmouth.edu/~carlp/PDF/paper101.pdf.
- ^ a b Banks, W. D.; Luca, F.; Shparlinski, I. E. (2007), "Estimates for Wieferich numbers", The Ramanujan Journal (Springer) 14 (3): 361–378, doi:10.1007/s11139-007-9030-z, http://web.science.mq.edu.au/~igor/Wieferich.pdf.
- ^ a b The Prime Glossary: Wieferich prime, http://primes.utm.edu/glossary/xpage/WieferichPrime.html
- ^ Israel Kleiner (2000), "From Fermat to Wiles: Fermat's Last Theorem Becomes a Theorem", Elem. Math. 55: 21, http://math.stanford.edu/~lekheng/flt/kleiner.pdf.Archived at WebCite
- ^ Leonhard Euler (1736), "Theorematum quorundam ad numeros primos spectantium demonstratio", Novi Comm. Acad. Sci. Petropol. 8: 33–37, http://math.dartmouth.edu/~euler/pages/E054.html.
- ^ Wieferich, A. (1909), "Zum letzten Fermat'schen Theorem", Journal für die reine und angewandte Mathematik 136 (136): 293–302, doi:10.1515/crll.1909.136.293, http://gdz.sub.uni-goettingen.de/dms/resolveppn/?PPN=GDZPPN002166968.
- ^ Coppersmith, D. (1990), "Fermat's Last Theorem (Case I) and the Wieferich Criterion", Math. Comp. (AMS) 54 (190): 895–902, JSTOR 2008518, http://www.ams.org/journals/mcom/1990-54-190/S0025-5718-1990-1010598-2/S0025-5718-1990-1010598-2.pdf.
- ^ Cikánek, P. (1994), "A Special Extension of Wieferich's Criterion", Math. Comp. (AMS) 62 (206): 923–930, JSTOR 3562296, http://www.ams.org/journals/mcom/1994-62-206/S0025-5718-1994-1216257-9/S0025-5718-1994-1216257-9.pdf.
- ^ Mirimanoff, D. (1910), "Sur le dernier théorème de Fermat", Comptes rendus hebdomadaires des séances de l'Académie des Sciences 150: 293–206.
- ^ Morishima, T. (1935), "Ueber die Fermatsche Vermutung. XI" (in German), Jap. J. Math. 11: 241–252
- ^ Granville, A.; Monagan, M. B. (1988), "The First Case of Fermat's Last Theorem is true for all prime exponents up to 714,591,416,091,389", Transactions of the American Mathematical Society 306 (1): 329–359, http://www.ams.org/journals/tran/1988-306-01/S0002-9947-1988-0927694-5/S0002-9947-1988-0927694-5.pdf.
- ^ Charles, D. X. On Wieferich primes
- ^ Mersenne Primes: Conjectures and Unsolved Problems, http://primes.utm.edu/mersenne/index.html#unknown
- ^ Kures, M. Wieferich primes and Mersenne primes
- ^ Ribenboim, Paulo (1991), The little book of big primes, New York: Springer, p. 64, ISBN 038797508X, http://books.google.com/?id=zUCK7FT4xgAC&pg=PA64
- ^ Wells Johnson (1977), "On the nonvanishing of Fermat quotients (mod p)", J. Reine angew. Math. 292: 196–200, http://www.digizeitschriften.de/index.php?id=resolveppn&PPN=GDZPPN002193698
- ^ Dobeš, Jan; Kureš, Miroslav (2010), "Search for Wieferich primes through the use of periodic binary strings", Serdica Journal of Computing 4: 293–300.
- ^ Keller, Richstein (2004), p. 930
- ^ Meissner, W. (1913), "Über die Teilbarkeit von 2p − 2 durch das Quadrat der Primzahl p=1093", Sitzungsber. D. Königl. Preuss. Akad. D. Wiss. (Berlin) Zweiter Halbband. Juli bis Dezember: 663–667
- ^ Beeger, N. G. W. H. (1922), "On a new case of the congruence 2p − 1 ≡ 1 (p2)", Messenger of Mathematics 51: 149–150, http://www.archive.org/stream/messengerofmathe5051cambuoft#page/148/mode/2upArchived at WebCite
- ^ Lehmer, D. H. (1981-01), "On Fermat's Quotient, Base Two", Math of Comp (AMS) 36 (153): 289–290, http://www.ams.org/journals/mcom/1981-36-153/S0025-5718-1981-0595064-5/S0025-5718-1981-0595064-5.pdf, retrieved 2011-04-22.
- ^ a b Ribenboim, Paulo (2004), Die Welt der Primzahlen: Geheimnisse und Rekorde, New York: Springer, p. 237, ISBN 3540342834, http://books.google.de/books?id=-nEM9ZVr4CsC&pg=PA237
- ^ a b c Dorais, F. G.; Klyve, D. (2011). "A Wieferich Prime Search Up to 6.7×1015". Journal of Integer Sequences (Journal of Integer Sequences) 14 (9). http://www.cs.uwaterloo.ca/journals/JIS/VOL14/Klyve/klyve3.pdf. Retrieved 23-10-2011.
- ^ PrimeGrid Announcement of Wieferich and Wall-Sun-Sun searches
- ^ a b Crandall, Richard E.; Dilcher, Karl; Pomerance, Carl (1997), "A search for Wieferich and Wilson primes", Math. Comput. 66 (217): 433–449, doi:10.1090/S0025-5718-97-00791-6, http://gauss.dartmouth.edu/~carlp/PDF/paper111.pdf.
- ^ Joshua Knauer; Jörg Richstein (2005), "The continuing search for Wieferich primes", Math. Comp. 74 (251): 1559–1563, doi:10.1090/S0025-5718-05-01723-0, http://www.ams.org/journals/mcom/2005-74-251/S0025-5718-05-01723-0/S0025-5718-05-01723-0.pdf.
- ^ About project Wieferich@Home
- ^ Ribenboim, Paulo (2000), My numbers, my friends: popular lectures on number theory, New York: Springer, pp. 213–229, ISBN 9780387989112
- ^ Wilfrid Keller; Jörg Richstein (2005), "Solutions of the congruence ap−1 ≡ 1 (mod pr)", Math. Comp. 74 (250): 927–936, doi:10.1090/S0025-5718-04-01666-7, http://www.ams.org/journals/mcom/2005-74-250/S0025-5718-04-01666-7/S0025-5718-04-01666-7.pdf.
- ^ Weisstein, Eric W., "Double Wieferich Prime Pair" from MathWorld.
Further reading
- Haussner, R. (1926), "Über die Kongruenzen 2p-1-1 ≡ 0 (mod p2) für die Primzahlen p=1093 und 3511", Archiv for Math. og Naturvidensk 39 (5): 7, http://jfm.sub.uni-goettingen.de/cgi-bin/jfmen/JFM/en/quick.html?first=1&maxdocs=20&type=html&an=JFM%2052.0141.06&format=complete
- Haentzschel, E. (1925), "Über die Kongruenz 21092 ≡ 1 (mod 10932)", Jahresbericht D. M. V. 34: 184, http://www.emis.de/cgi-bin/JFM-item?51.0128.*
- Bray, H. G.; Warren, L. J. (1967), "On the square-freeness of Fermat and Mersenne numbers", Pacific J. Math. 22 (3): 563–564, MR0220666, Zbl 0149.28204, http://projecteuclid.org/DPubS?service=UI&version=1.0&verb=Display&handle=euclid.pjm/1102992105
- Silverman, J. H. (1988), "Wieferich's criterion and the abc-conjecture", Journal of Number Theory 30 (2): 226–237, doi:10.1016/0022-314X(88)90019-4
- Ribenboim, P. (1979), Thirteen lectures on Fermat's Last Theorem, Springer-Verlag, pp. 139, 151, ISBN 0-387-90432-8
- Guy, Richard K. (2004), Unsolved Problems in Number Theory (3rd ed.), Springer Verlag, p. 14, ISBN 0387208607
- Garza, G.; Young, J. (2004), "Wieferich Primes and Period Lengths for the Expansions of Fractions", Math. Mag. 77 (4): 314–319, doi:10.2307/3219294, JSTOR 3219294
- Crandall, R. E.; Pomerance, C. (2005), Prime numbers: a computational perspective, Springer Science+Business Media, Inc., pp. 31–32, ISBN 0-387-25282-7, http://books.google.com/?id=RbEz-_D7sAUC&pg=PA31&dq=wieferich+prime#v=onepage&q=wieferich%20prime&f=false
- Ribenboim, P. (1996), The new book of prime number records, Springer-Verlag New York, Inc., pp. 333–346, ISBN 0-387-94457-5, http://books.google.com/?id=72eg8bFw40kC&pg=PA333&dq=wieferich+prime#v=onepage&q=wieferich%20prime&f=false
External links
- Weisstein, Eric W., "Wieferich prime" from MathWorld.
- Fermat-/Euler-quotients (ap−1 − 1)/pk with arbitrary k
- A note on the two known Wieferich primes
|
|||||||||||||||||||||||||||||